Kernel-less eigensystem

There’s a neat question one can ask about anisotropic Gaussian data on kernels: for a general kernel, what should we expect the eigenfunctions to look like? How much do we even need to worry about the specifics of any kernel? The answer is, surprisingly, not much… let’s go through it. You can broadly say, “well, the kernel should be able to represent any polynomial of the data,” so we can separate out the features into different levels representing the orders of the polynomials. I’ll give the first one as a freebe as I didn’t motivate it all that much:

• Const mode: $\lambda$ = 1, $\phi(\vec{x})$ = 1

from there on, we can guess that the data $x_i \sim \mathcal{N}(0, \gamma_i)$ itself (ie a linear function of the data) will be a feature²:

• Linear modes: $\lambda$ = $\gamma_i$, $\phi(\vec{x})$ = $x_i$.

From here on, I hope the pattern has become more obvious, with the next level being…

• Quadratic modes: $\lambda$ = $\gamma_i\gamma_j$, $\phi(\vec{x})$ = $x_ix_j$
• Cubic modes: $\lambda$ = $\gamma_i\gamma_j\gamma_k$, $\phi(\vec{x})$ = $x_ix_jx_k$

Kernel eigensystem

The above picture obviously misses some things, namely the kernel itself. However, our guess is surprisingly close to the real kernel eigensystem!

Eigenvalue fix

To incorporate the kernel, write out the kernel function as a Taylor series expansion:

with this epansion working so long as the points $\vec{x}$ and $\vec{x}'$ have roughly the same magnitude, $|\vec{x}| \approx |\vec{x}'| \equiv r_0$. This turns our rotation-invariant kernel into a dot-product kernel! Being able to express a rotation-invariant kernel as a dot product one is equivalent to having datapoints $\vec{x}$ lie along a hyperellipsoid that “looks spherical enough:” we don’t need the data to exactly lie on the sphere, but if one direction (ie $x_0$) holds much more weight than the others, then the data lies more along a line than a sphere, and the expansion breaks. We can start to see where the eigenvalue fix kicks in: let’s take a linear mode $x_i$ to be our eigenfunction we want the eigenvalue of. In the expansion, this will (at least shortly if you’re familiar enough with Guassian distributions) select out only the $x_i^\top x_i'$ part of the $(\vec{x}^\top \vec{x}')^\ell$ equation:

where we can see the only fix we need to make to the eigenvalues are to add on an additional factor of $c_\ell$ to the eigenvalues at level $\ell$.

In a future update, I will give a small preview of how to obtain these “level coefficients” $c_\ell$.

One of the amazing things here is that this is direction-independent so all eigenvalues within a level are affected by the same factor³, and to give a bit of a spoiler, this is the only place the kernel appears! The eigenfunctions need to be fixed in a very simple way:

Eigenfunction fix

The functions $\phi(\vec{x})$ = $\prod_\alpha x_\alpha$ for some general index-selecting object $\alpha$ need to be changed so that they’re actually eigenfunctions: they must be an orthonormal basis.

To start, $x_\alpha^2$ will be on average $\gamma_\alpha$, not $1$, so the first thing to do is to have $\phi(\vec{x})$ = $\prod_\alpha x_\alpha/\gamma_\alpha$.

The second thing to do is to verify these are actually orthogonal to each other: $\int_{\vec{x}\sim\mu} \text{d}\vec{x} \phi_i(\vec{x})^\top\phi_j(\vec{x}) = \delta_{ij}$. This will not be true when there are repeated indices, $\vec{x}_i^2$ isn’t orthogonal to $1$, at least when the data is Gaussian-distributed! To get around this, we can simply subtract off whatever the overlapping component is, so $\phi(\vec{x}) = x_i^2/\gamma_i \rightarrow (x_i^2-1)/\gamma_i$. If we continue this pattern (the linear and cubic modes overlap, quadratic and quartic, etc.) then we get the Hermite polynomials.

The Hermite Eigenstructure Ansatz

We can now state the main takeaway of our paper:

Take any rotation-invariant kernel with high-dimensional Gaussian data. The eigensystem of this kernel will be approximately the same as if the eigenvalues and eigenfunctions were given by,

• $\lambda_i = c_\ell \prod_i \gamma_i^{\alpha_i}$
• $\phi_i(\vec{x}) = \prod_i$ $h_{\alpha_i}(x_i/\gamma_i)$

where $\alpha \in \mathbb{N}^d$, $\sum_i \alpha_i = \ell$, and $h$ are the (probabilist’s) Hermite polynomials. We call this the Hermite Eigenstructure Ansatz (HEA), “ansatz” here roughly translated to “approximation” or “guess”.

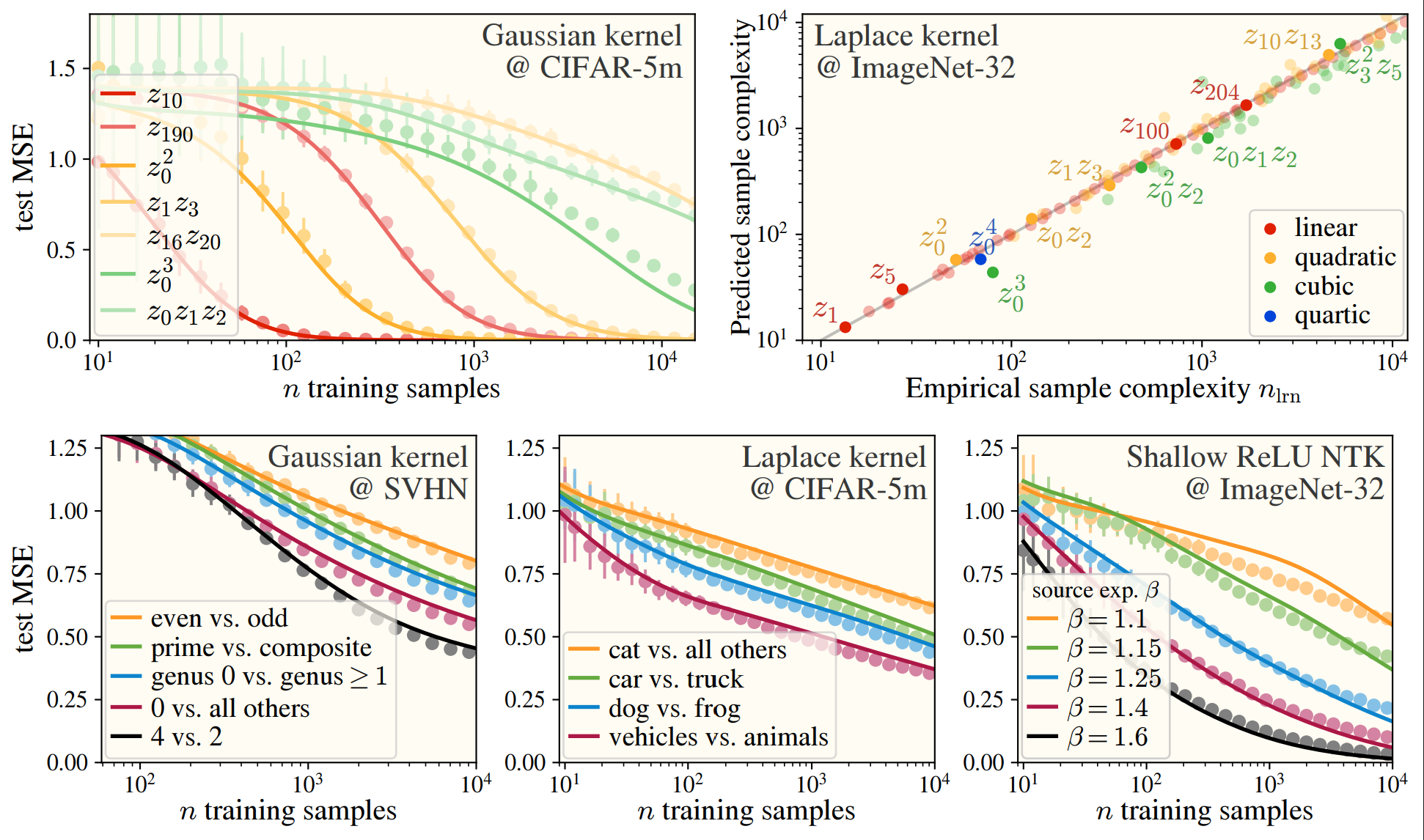
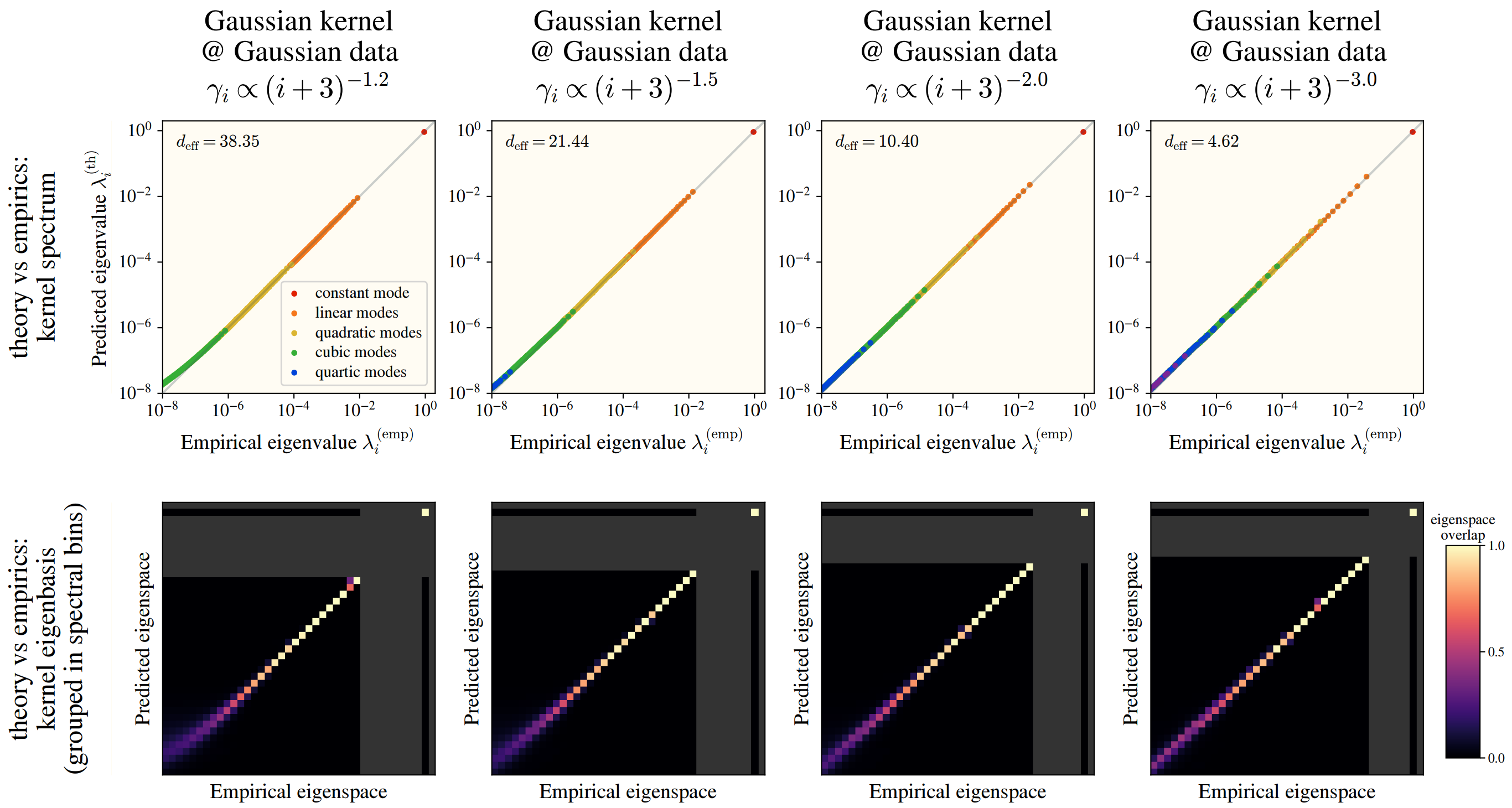
Checking this numerically, we see a fantastic overlap between the HEA and a real kernel eigensystem:

This works among numerous kernels and on real datasets: CIFAR10, SVHN, and ImageNet! In the images, we see how well the $i$-th eigenvalues are approximated by the HEA (top), and the similarity between the HEA-predicted and real eigenvectors (bottom), where we have binned eigenvectors into an “eigenspace” for visual clarity.

The HEA is a guess

Of course, we can’t prove exactly how anything (other than maybe linear regression) performs on real data—there’s a reason we call this the Hermite Eigenstructure Ansatz and not the Hermite Eigenstructure Equivalence. The HEA starts to break down once we get further from the nice land of theory, with 3 key points being required on the data and the kernels: the data lies on something like a hypersphere, the level coefficients $c_\ell$ decay quickly enough, and the data is We can exactly prove that this Hermite eigensystem is the true eigensystem if we “inverse” these conditions. In slightly more detail,

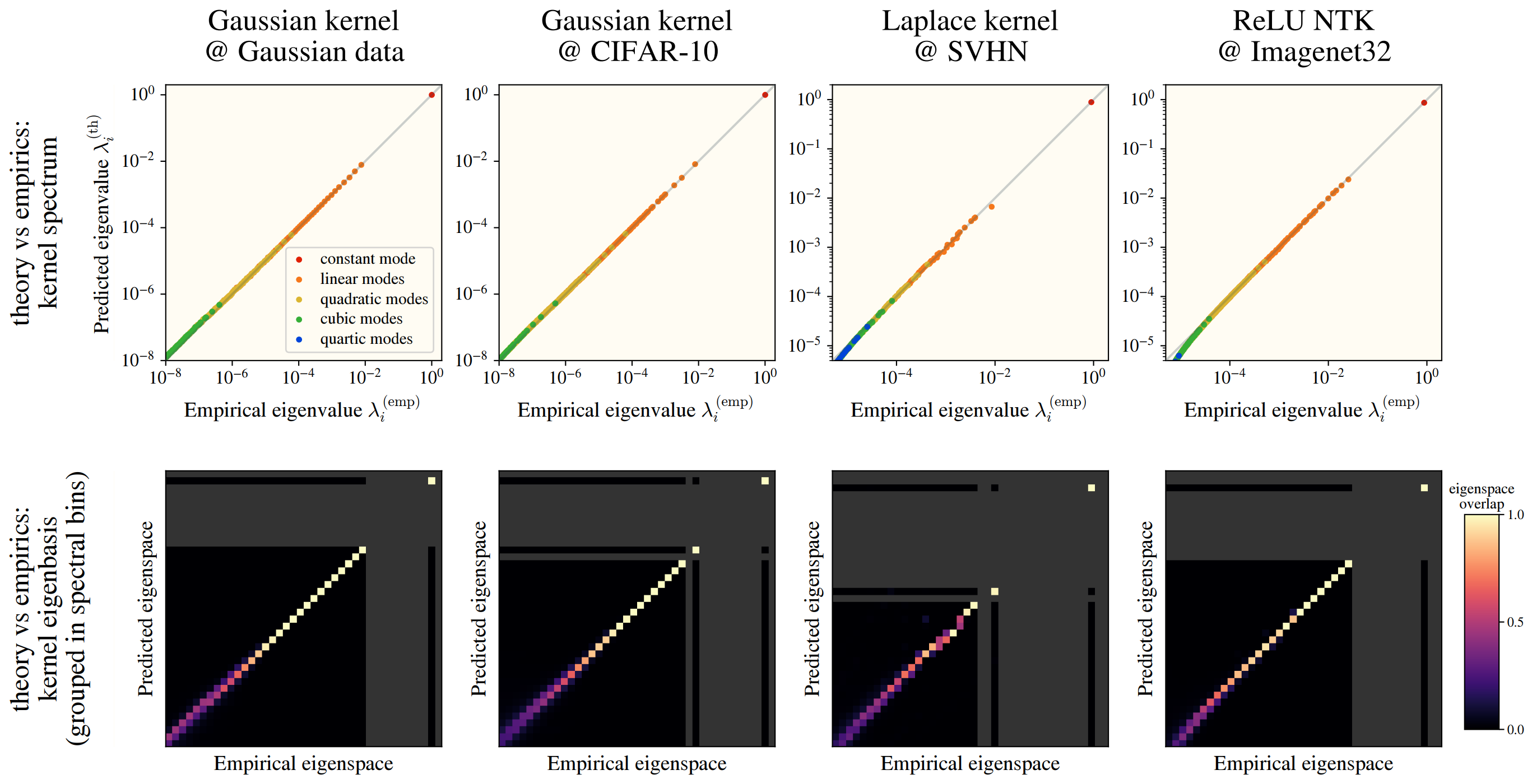
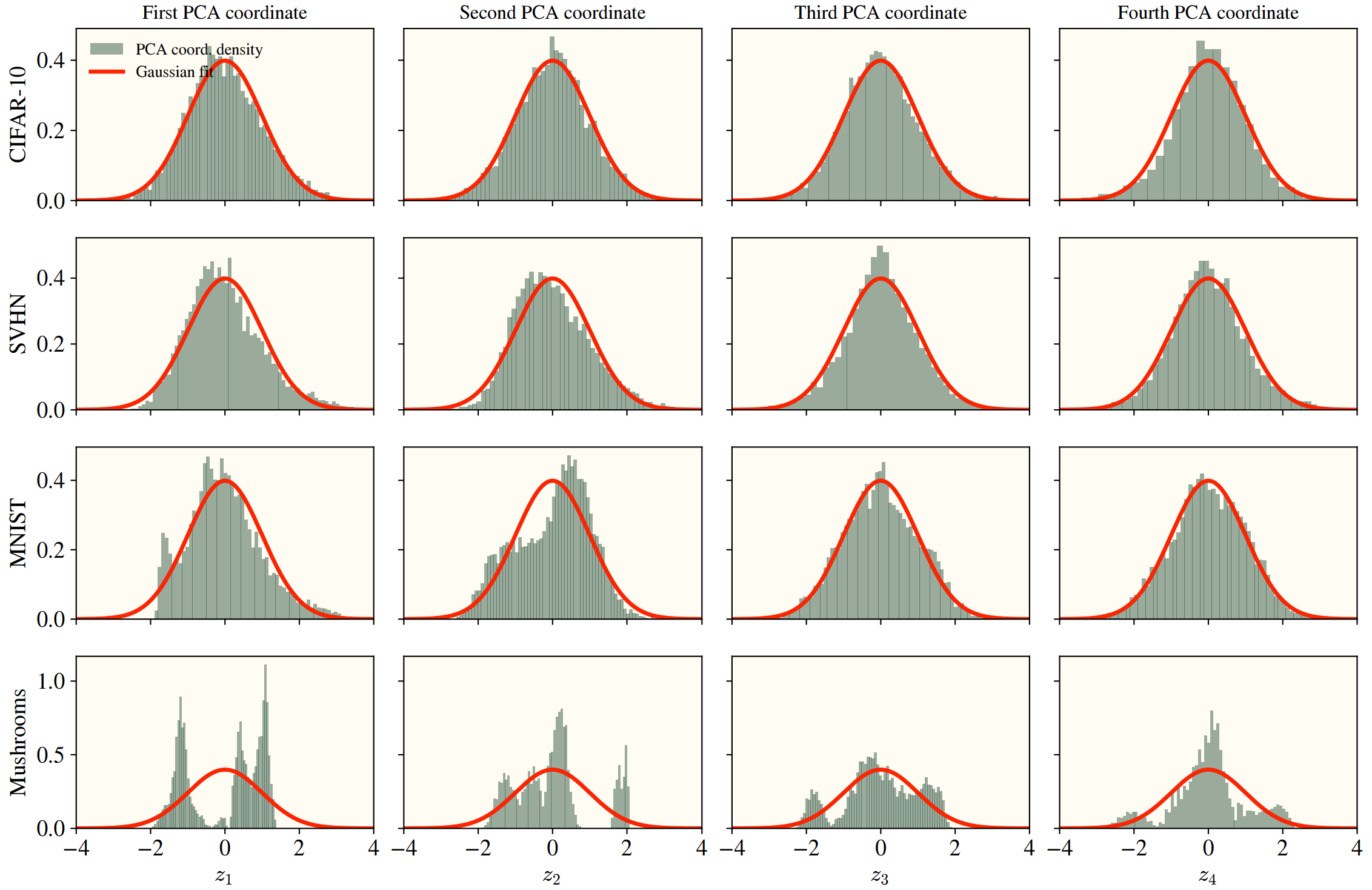
1. (High data dimension) If the data is inherently low dimensional, or if a few directions contribute the most to the data’s variance, then the HEA starts breaking down. If there are preferred directions, then the prefactors $c_\ell$ wouldn’t just depend on the level, and there’s no guarantees the eigenfunctions will be our simple hermites. Certain datasets (namely categorical, see “Mushrooms”) have a few preferred directions, with the exact eigenstructure differences shown below.

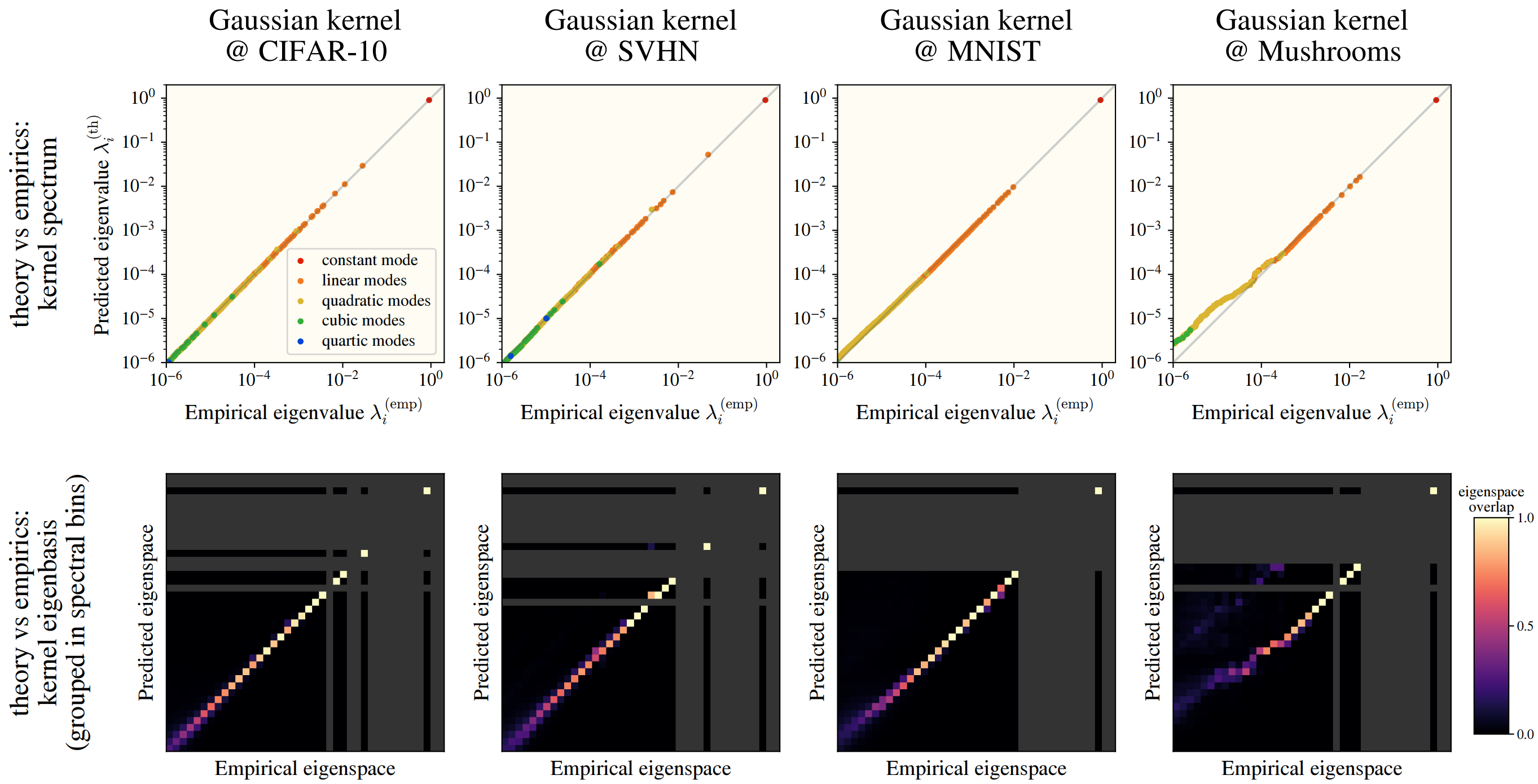
2. (Fast level coefficient decay) If the level coefficients are “close” to each other, then we get a strange effect: to recover our eigenfunctions as Hermites, we made $\phi(x_i^d)$ orthogonal to $\phi(x_i^{d+2})$. That, however, was under the assumption that the eigenvalue corresponding with the degree $d$ polynomial was much larger than the $d+2$ polynomial; when this breaks, we end up with a bit of “mutual-orthonormalization” where both the degree $d$ and $d+2$ terms interact and try to orthonormalize against the other. In practice, we can sometimes fix this problem by just making the kernel wider; otherwise, the dataset is simply not good for our kernel and HEA.

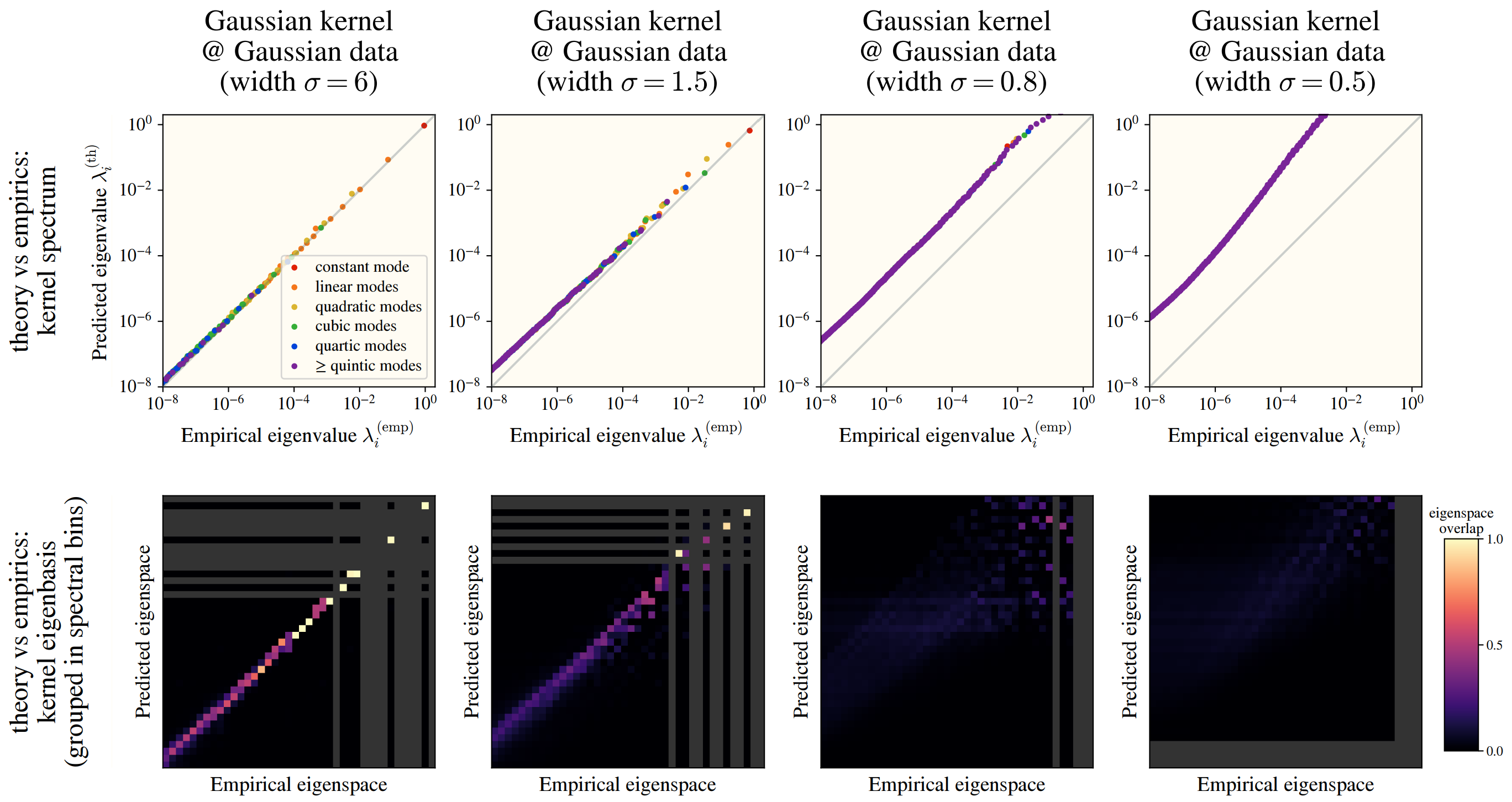
Above, we see that changing the Gaussian kernel’s width $\sigma$ can drastically affect how well the HEA works.

Whereas changing the dataset size itself barely changes anything!

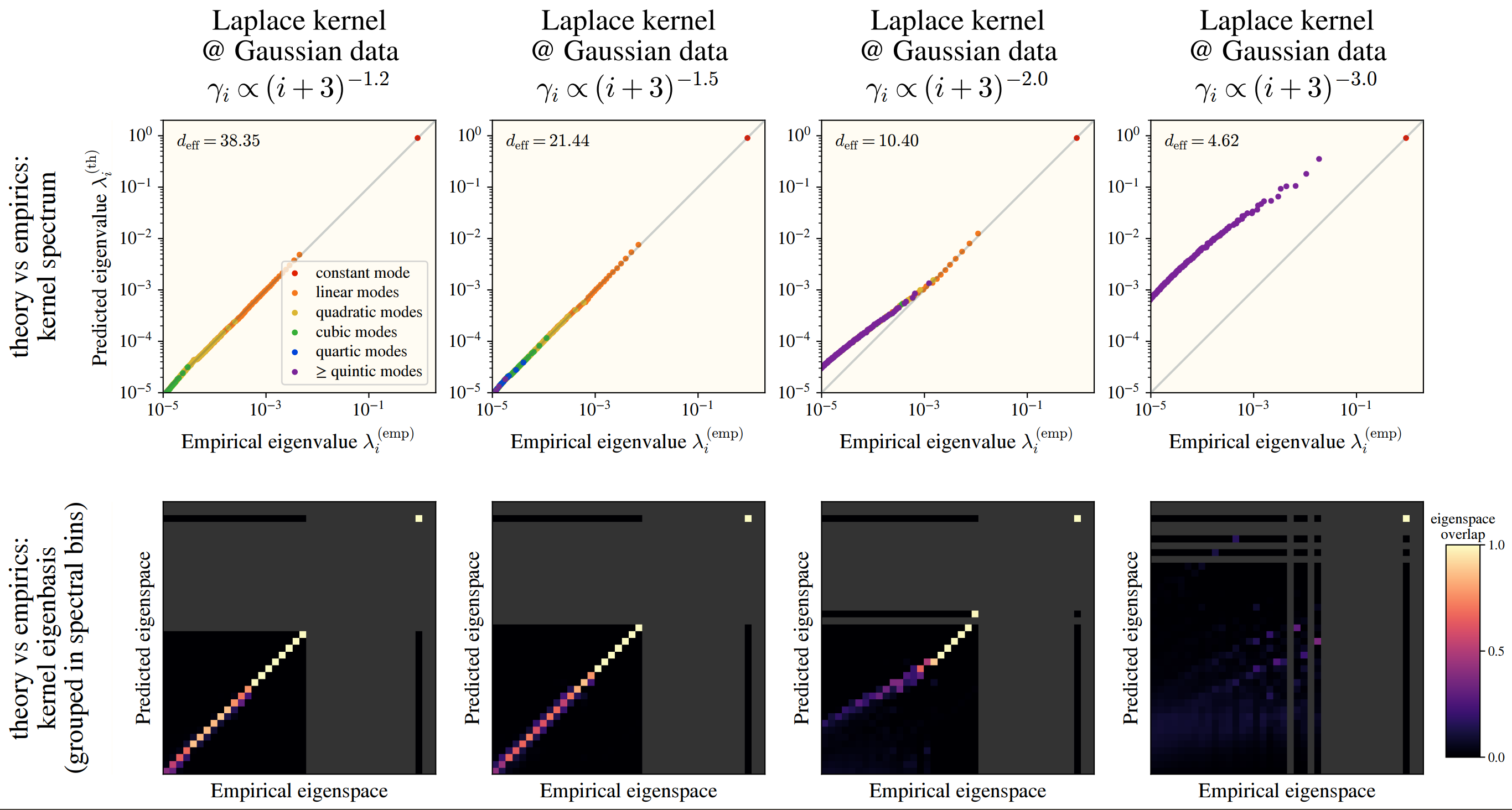
Although this is not true for all kernels! If we take the Gaussian (or ReLU NTK), then the data is far more important!

3. (Gaussian data) As stated earlier, we need Gaussian data with known covariances—this clearly isn’t true in real settings, so how far does it go if the data isn’t Gaussian? The HEA actually works quite well, unless the PCA components are heavily dependent⁴ or the marginals are far from being approximated by Gaussian. Independence is hard to visualize, but below I’ve given examples of data that’s far from Gaussian.

HEA to predict learning curves

Now we can get to the real takeaway: as we can predict the eigenstructure of the data, we can take our favorite kernel learning curve theory paper (ie (Simon et al., 2021)), and directly predict what the test error, train error, error of specific components, etc. is, or how many samples we need to get below a certain error!

While I’d recommend reading any one of the kernel learning curve theory papers to get a better idea of what’s going on under the hood, I’ll highlight one thing here: the kernel learns the top $n$ eigenfunctions when presented with $n$ samples. Combined with the HEA, we can get a striking observation, if $c_6 \gamma_i^6$ > $c_1 \gamma_j$, then the sixth-order function corresponding with $x_i^6$ will be learned before the linear function $x_j$!

The HEA moving forward

Let’s step back for a little bit. Why should the HEA be at all useful moving forward?

My response: I’ve checked how fast feature-learning networks learn each term in the polynomial expansion of data, and found that the HEA eigenvalues are incredibly predictive of how long it takes a network to learn its corresponding term:

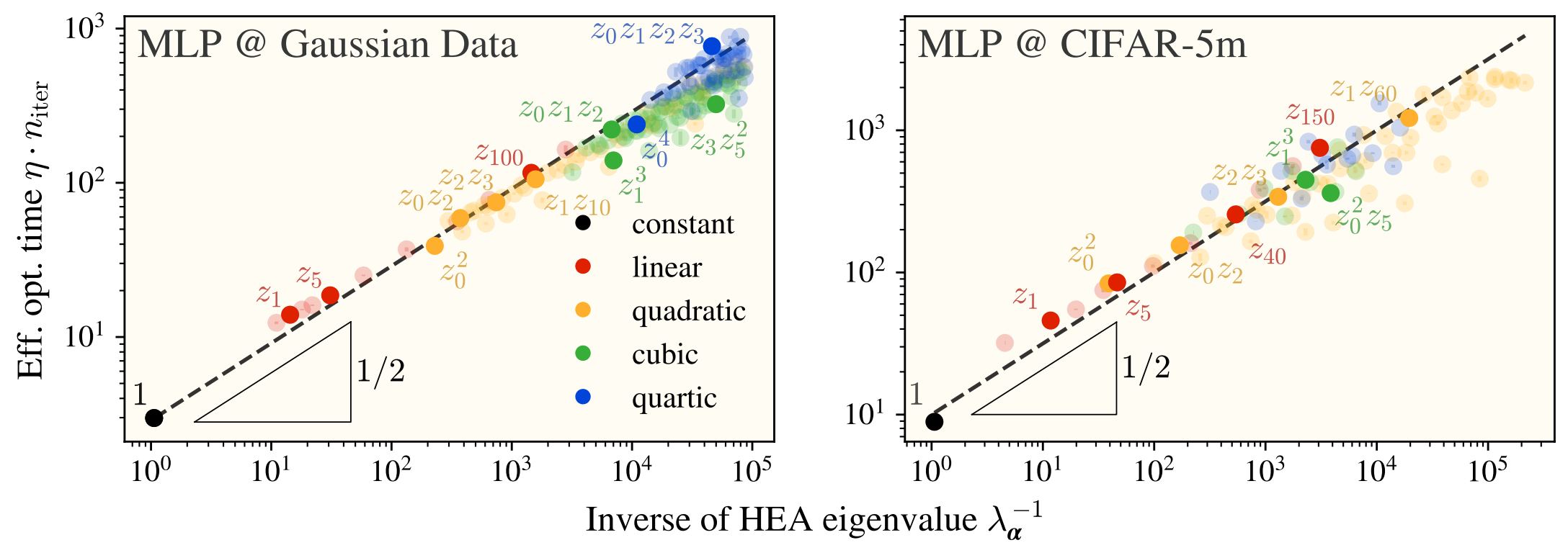
where we’re currently working on understanding where the $1/2$ factor comes from.

Afterword

From here, we’re taking a detour away from kernels and putting a much heavier focus on feature-learning MLPs. If you have questions or comments about any of the content on this page, please feel free to reach out to me! Thanks for reading!

References